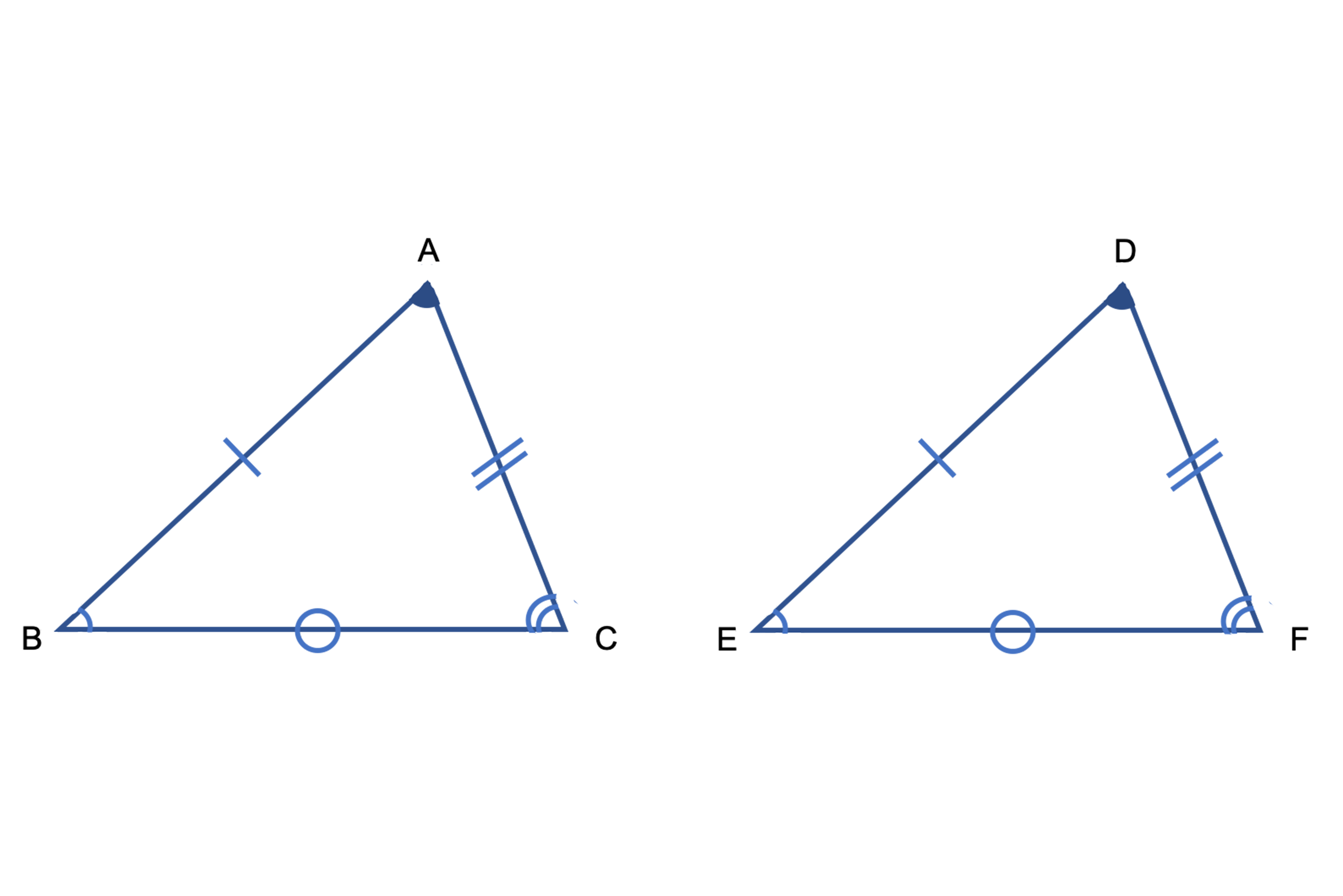
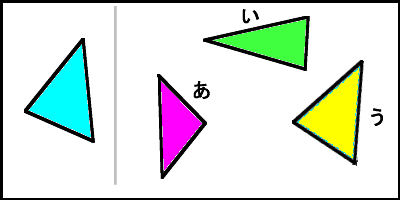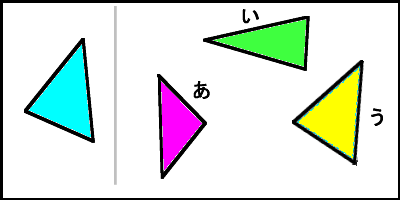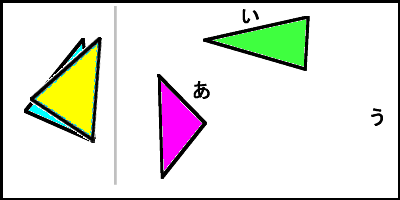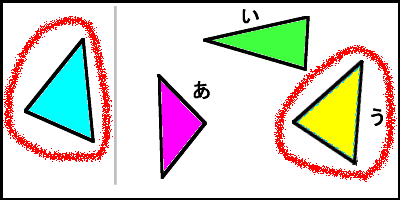
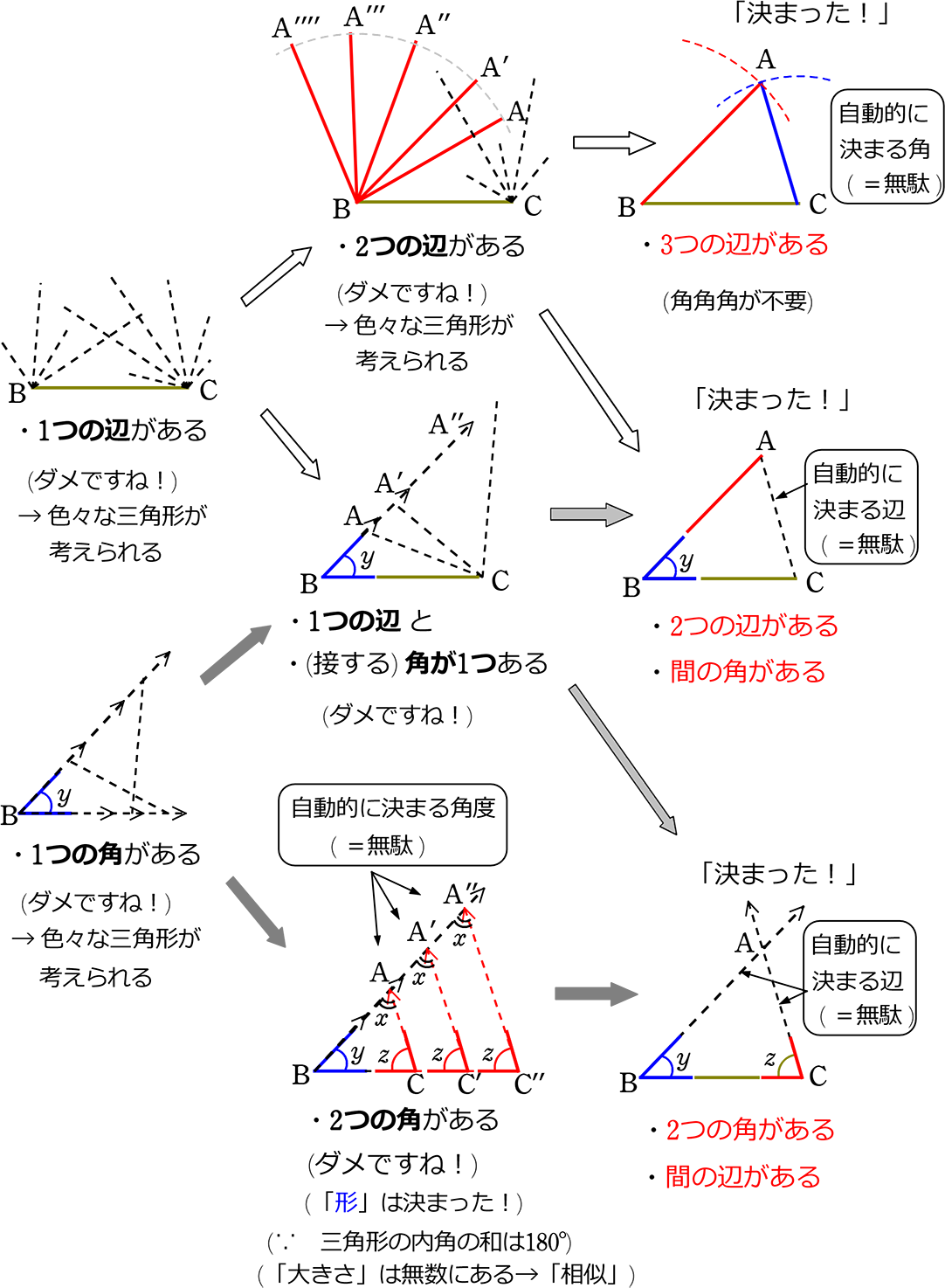
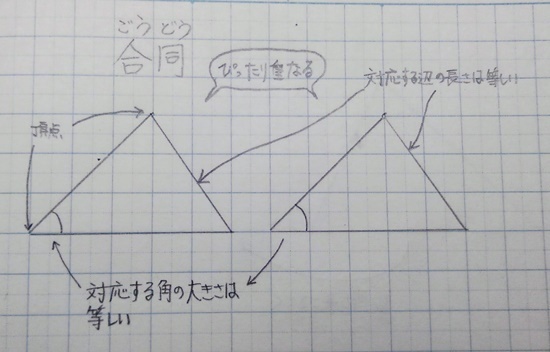
3つの角がそれぞれ等しい三角形は・・・ 辺の長さが違うかもしれないから合同になるとは限らない。 3つの辺の長さがそれぞれ等しい三角形は・・・ このどちらかにしかならないから合同だね。 2つの辺と1つの角がそれぞれ等しい三角形は・・・ こんな三角形になるかもしれないから合同に 合同では角の大きさと合わせて辺の"長さ"に注目しましたが、相似では辺の"比"に着目します。相似の場合、対応する辺の比は全部同じです。「相似比」と呼ばれますが、上の画像にある三角形の場合は abcと defの相似比は、 abc: def= 12になります。下の図形は、同じ色の図形どうしが合同です。 その理由をお子さんに言わせてみましょう 辺の長さや角の大きさに注目して、考えを言えたらほめてあげてください。 教え方3 このことを通して、「合同な図形の性質」は、 ①対応する線分の長さは等しい。
5年算数合同な図形 わかる教え方
図形の合同と角 ict
図形の合同と角 ict-「合同な図形」では,合同な三角形を描く手順について,辺の長さや角の大きさといっ た構成要素に着目しながら,仲間と意見を出し合い3通りの描き方があることを明らかに した。その後,自分で決めた描きやすい方法で様々な条件の三角形を描くことができるよ うになった。また,「合同合同な三角形を探そう(図形の合同) 三角形の角の応用1(ちょうの形)(図形の角) 三角形の角の応用2(ブーメランの形)(図形の角) 三角形の角の応用3(星の形)(図形の角) 何度になるかな?(図形の角) 折り紙遊び(図形の角) 合わせて何度?(図形の角) 世界一の花時計 (円




世界一分かりやすい算数 小5 合同な図形
角の大きさの求め方を、補助線や根拠となる図形の性質を明らかにして説明する。 9 既習事項を活用していろいろな問題を解く。 10 合同な図形の表し方を理解する。 合同な図形の性質を見いだす。 11②合同な図形では、対応する角の大きさ は等しい。 合同な三角形を掲示し、それぞれ対応す る辺、角の大きさが等しいときが合同で あることを確認させる。 合同な図形の性質を確認し、合同な図形 をかくためには線分、角の大きさを調べ る必要があることにつなげる。 展開 5人ずつのけでなく, 図形の角の大きさに着目して, 図形を多面的に考察することに課題があった。 「合同な図形」の学習では, ぴったりと重ね合わせることができる2つの図形を合同な図 形と定義した。しかし, 図形の合同を判断する際に, 正三角形やひし形など図形の性質に着 目して判断することが不
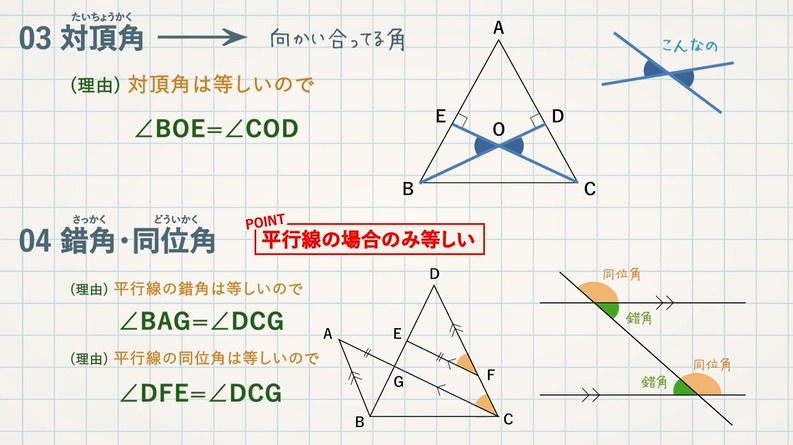
『合同な図形は、対応する角の大きさが等しい』 ということを覚えておくだけで解けちゃう問題です。 ∠gと対応する角は∠bです。 よって、∠gと∠bは同じ大きさになるので 答え $$\large{∠g=60°}$$ 合同な三角形の見つけ方とは? さて、ここまで合同な図形の性質についてお話をしてきました対頂角・同位角・錯角の性質と簡単な覚え方 管理人 2月 17, 19 直線同士のなす角には「対頂角」「同位角」「錯角」という特別な関係があります。 これらは重要な性質があり、今後図形の角度の大きさを求める問題や合同の証明などに頻繁に使うことに角について理解する。 方眼を使って,合同な図形の 作図を行う。 合同な図形の性質を調べる活 動を通して,図形を回転させた り裏返したりして対応する頂点,辺,角について理解する。 方眼を使って,頂点を確認し ながら,合同な図形の作図を行 う。
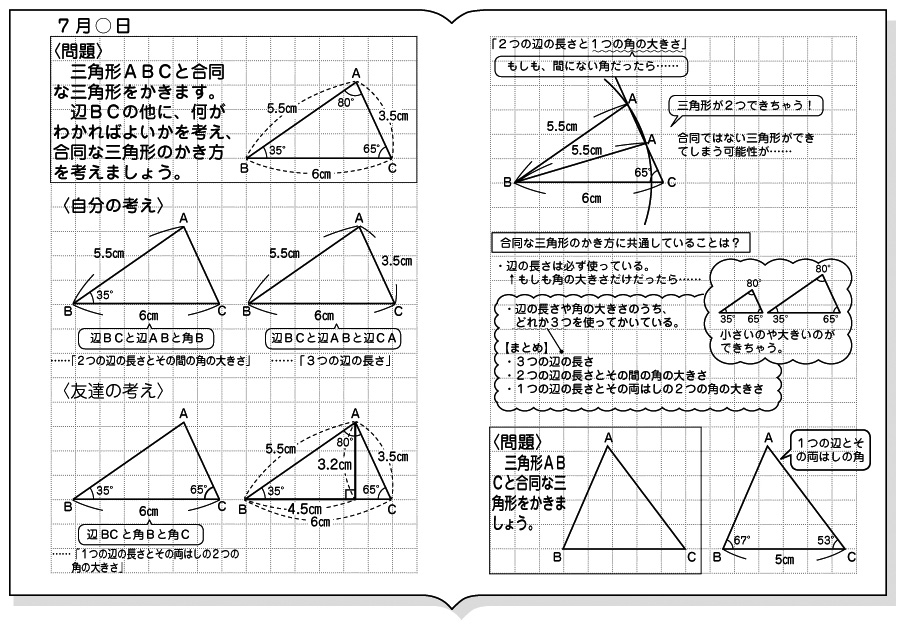
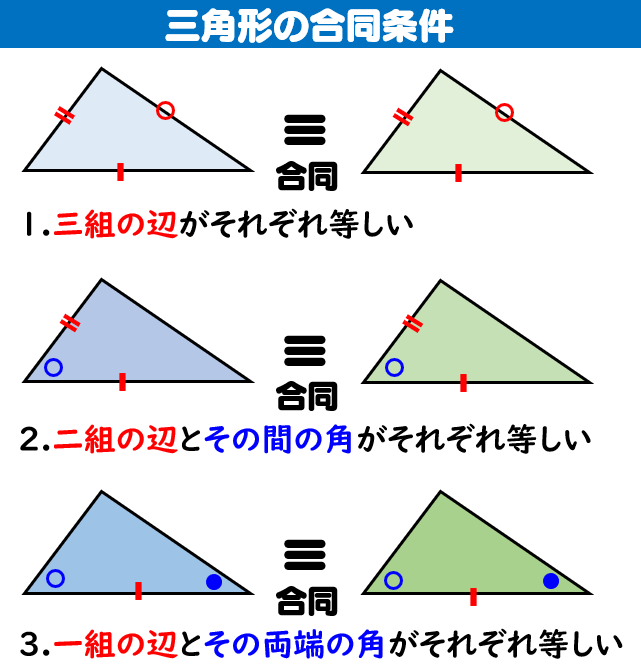
5年「合同な図形 必要な辺と辺,角と角の対応が付けられる ようにすることが大切になってくる。 またr中学校学習指導要領解説 数学 編Jには,次の様に示されている。 B 図形 ( 1 )観察,操作や実験などの活動を 通して,見通しをもって作図し たり図形の関係について調べた りして平面合同と角 の単元において図形の敷き詰めを計画的に組織し実践を行うこととする。その実践の中から,敷き詰めの 活動でどのように四角形の認識が深まるかを確かめ,敷き詰めの活動はどのように進めていったらいいのかの方法を 探ることとする。 敷き詰めに対する県内児童の認識度と学習角 ・合同な図形の合同であることや、辺や角の関係などを記 形 号を用いて表したり、その意味を読み取ったりすること の ができる。〔観察、ノート〕 合 9 三角形の合同条件 ・2つの三角形がどんな場合に合同になるかを考え、合同であ




中2数学 平行なときの同位角 錯角 例題編 映像授業のtry It トライイット




スタディピア 図形
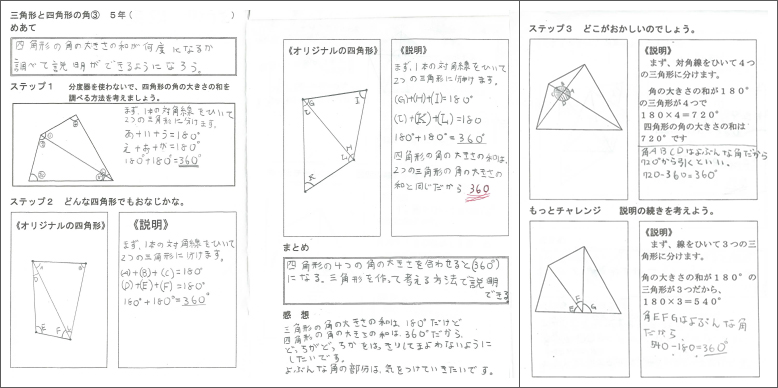
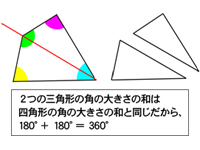
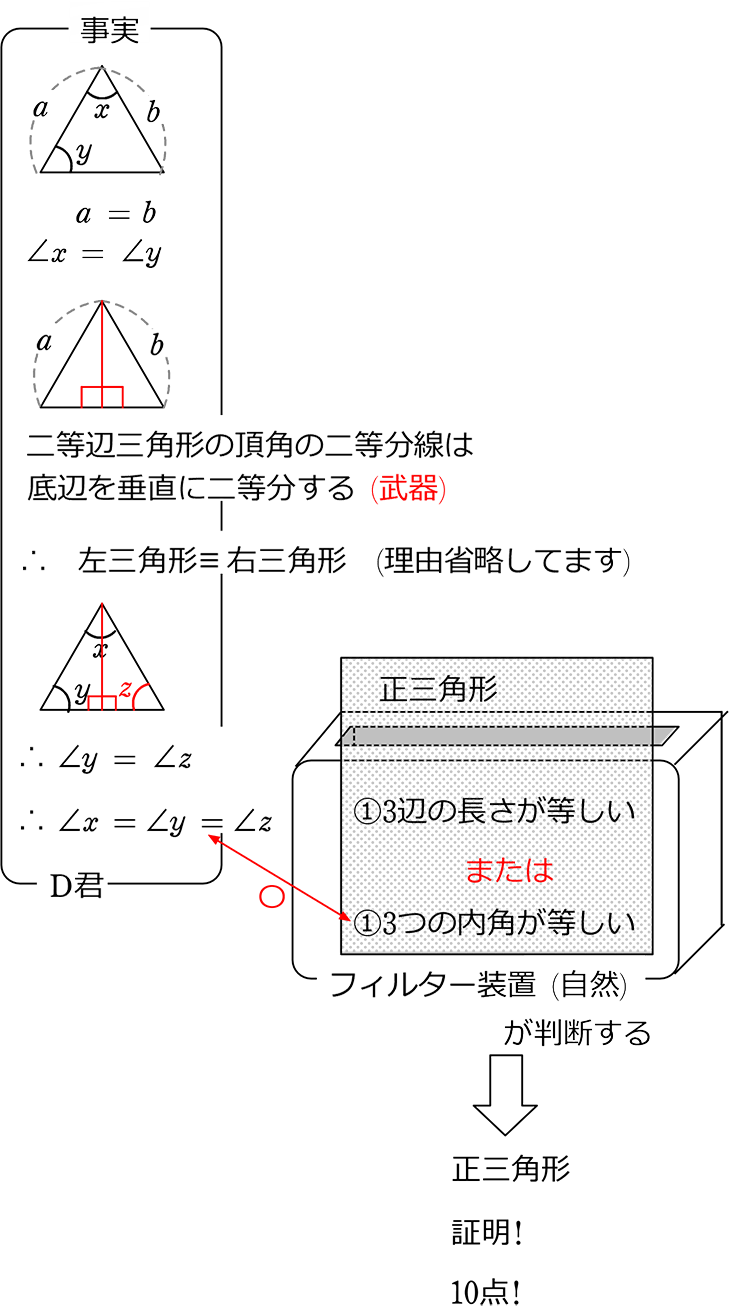
移動させることによって、重ね合わせることができる $2$ つの図形は 合同 である。 合同な図形の性質 ・対応する線分の長さはそれぞれ等しい。 ・対応する角の大きさはそれぞれ等しい。 $2$ つの図形が合同であることは、記号 「≡」 を使って表します。正三角形の3つの角の大きさは等しいこと は3年生,角の大きさは60°であること4年生の既習事項。 5年生の図形の合同の学習においても復習しているが正答率が 低い。 ③ 正答率 58.3% 角の大きさと回転の大きさの関連ができていない。ウ 図形の性質を見いだし、それを用いて図形を調べたり構成したりすること。 〔算数的活動〕(1)エ 三角形の三つの角の大きさの和が180°になることを帰納的に考え、説明する活動 四角形の四つの角の大きさの和が360°になることを演繹的に考え、説明する活動




中学校数学 2年生 図形 図形の調べ方 Wikibooks



小5算数 合同な図形 指導アイデア みんなの教育技術
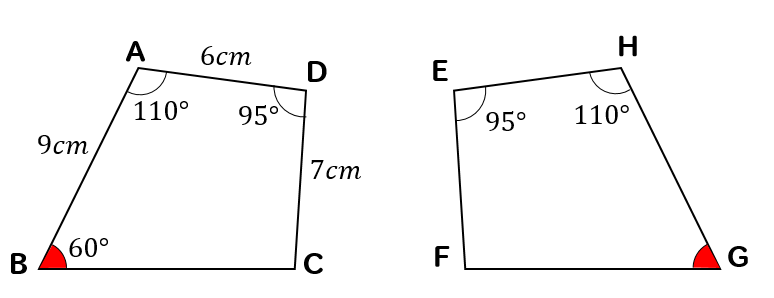
図形 定義・定理 まとめ 対頂角 𝟖は等しい 直線の角度 ° 平行線の 同位角 𝟖 は等しい 角形の内角の和 °×(𝒏− ) 平行線の 多角形の外角の和錯角 𝟔は等しい ° 同位角 が等しければ、2直線は平行 〇 合同な図形の対応する線分や角は等し星形の図形では 全ての角を足すと180°になります。 なぜ180°になるのか?というと 三角形の外角の性質を使いながら 全ての角を、1つの三角形に集めることができるからでしたね! 足したら180°! これさえ覚えておけば、問題を解くことは楽勝のはずです。 しっかりと覚えておきましょう同な図形の対応する頂点,対応する辺,対応する角という。 合同な図形では,対応する線分の長さは等しく,対応する角の大きさも等しい。 2 問題(2 学期期末) 右の図で abc≡ def とする。 (1) ab と対応する辺はどれか。 (2) ∠d の大きさを求めよ。 解答欄 (1) (2) 解答(1) de (2) 60° 三角形の合同




5年生 合同な図形の学習動画です たったこれだけプリントの14ページを見てください Youtube



重なる形と図形の角を調べよう 図形の角と合同 第5学年 小学校 算数 My実践事例 日本文教出版
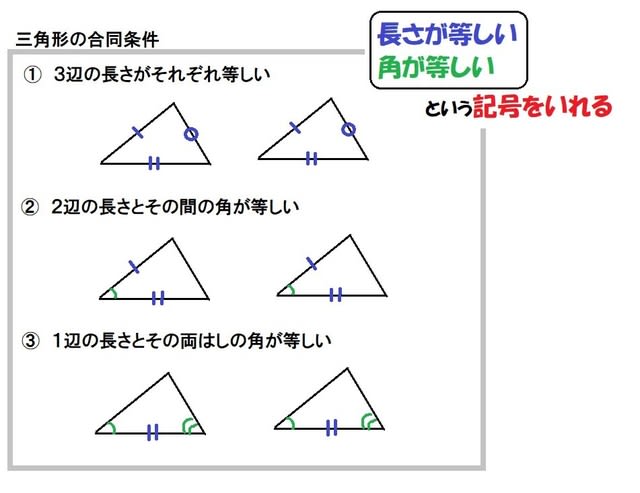
同位角に錯角、合同や三平方の定理などを日常生活に生かすことはできないだろうか。 (石川大樹) 図形の知識② <三角形の合同条件> 一組の辺とその両端の角がそれぞれ等しい 重ねて比較。この一辺の長さは3枚とも等しい。 その両端の角は、すべて70度。3枚のチップスの形はすべて合同実践記録算数5年 1.単元名 図形の角 2.単元の目標 既習図形の内角の和を使って,三角形や四角形などの角を調べる活動を通して,「三角形の内角の和のいくつ分」という考えのよさが分かり,これを用いて図形の角を調べることができる。 3.単元の表現・処理 ・必要な辺の長さや角の大きさを調べ,合同な図形を弁別したり,合同な三角 形などをかいたりすることができる。 知識・理解 ・合同な図形では,対応する辺の長さや角の大きさは等しいことを理解する。 0 367% 533% 267% 233% 600% 33% 0 2 4 6 8 10 12 14 16 18 あ き



中学数学 合同な図形の性質とは 見つけ方は 問題を使って解説 数スタ



小学5年生の算数 合同な図形の性質を知る 練習プリント ちびむすドリル 小学生
図形の相似の概念は図形の合同 ( r = 1 二角相等 (aa):2組の角がそれぞれ等しければ、2つの三角形は互いに相似である。 この条件を満たせば、残りの角の組も等しくなる。 三辺比相等 (sss):3組の辺の比が互いに等しければ、2つの三角形は互いに相似である。 二辺比夾角相等 (sas):2組の辺5年「図形の合同と角」(学校図書)を向山型算数で授業する TOSSインフィニット 篠 崎 孝 一 あなたは 人目のお客様です。00.8.04日更新 法則化運動がお嫌いな方・反法則化の方はご遠慮下さい 当ホームページへのリンクはフリーです。 小学5年生の「合同な図形」について、 ここで扱われている 三角形の合同 は 超重要 ですよ どれくらい重要であるかって 高校入試の数学の問題に出てきます



図形の合同と対応 算数用語集




世界一分かりやすい算数 小5 合同な図形
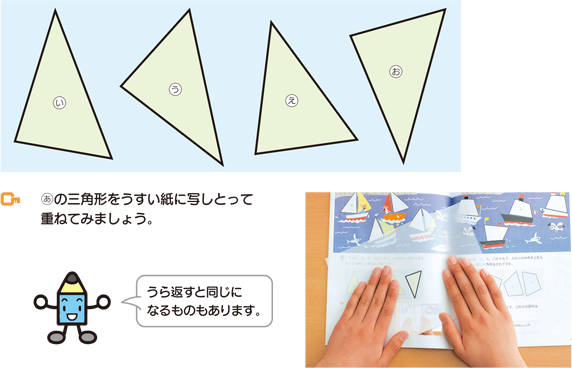
図形の合同と角 6 令和2年5月29日公開 第4地区 整数と小数のしくみをまとめよう 1 令和2年4月日公開 整数と小数のしくみをまとめよう 2 令和2年4月日公開 整数と小数のしくみをまとめよう 3 令和2年4月27日公開 整数と小数のしくみをまとめよう 4 令和2年4月27日公開 体積 1 令和2年5月11☆ 合同な図形 ⑩ 角の大きさ ・図形の合同 ・回転の角の大きさと単位 ・角度のはかり方,かき方 本単元 図形の角 ・三角形,四角形の内角の和 ・図形の性質 ・多角形や正多角形 4年 5年 6年 (2) 児童観 実践校の対象児童は,課題に取り組むとき既習事項を生かしてなんとか自力で解決しようと 「重なる形と図形の角を調べよう」 図形の角と合同 2.本時の位置づけ 第11時(全15時間) 3.本時のねらい 4.本時の評価規準 知識・理解 5.単元の指導計画 時 主な学習内容と活動(※主な算数的活動) スタイル 1 パズルで形を構成する活動や薄い紙に写して重ねる活動、身のま



重なる形と図形の角を調べよう 図形の角と合同 第5学年 小学校 算数 My実践事例 日本文教出版



合同な図形 小5 合同条件は超重要 算数の教え方教えますmother S Math Happy Study Support
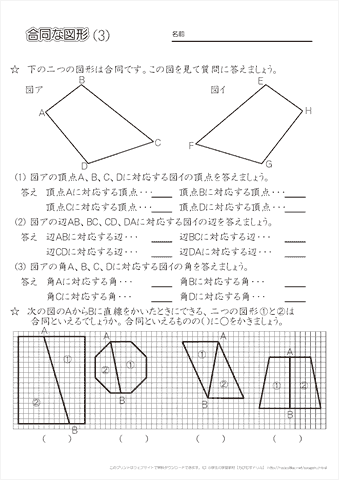
ユークリッド幾何学 において、二つの 図形 が 合同 (ごうどう、 英語 congruence )とは、それらの形と大きさが同じであるということを数学的に表した概念である。 場合によっては、形と大きさが同じである他に、一方が他方の 鏡像 である場合を含める 。よって、合同な図形の対応する角どうしは等しく、角bと角cについては、頂点bと頂点cが 式 abd ≡ acd の2番目にある文字であることからも分かるように角bと角cは合同図形の対応しあう点なので、 ∠ b = ∠ c である。 そして、この角bと角cはそもそも底角であったので、よって二等辺三角形の2つ・2つの合同な図形に おける頂点,辺,角 の対応について理解 する。 小学校第6学年 「対称な図形」 ・線対称及び点対称の 意味を知り,対称性 に着目して基本的な 図形を考察すること ができる。 中学校第1学年 「平面図形」 ・線分の垂直二等分線,角の二



合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典



合同な図形とは 三角形の合同条件 教遊者
・合同な図形のかき方 図形の角 ・三角形、四角形の内角の和 ・多角形の定義 ・多角形の内角の和 正多角形と円周の長さ ・正多角形の定義 ・正多角形の性質と作図 6年 対称な形 ・線対称、点対称の概念、性 質、かき方 ・対称性による多角形の考察 拡大図と縮図 ・拡大図
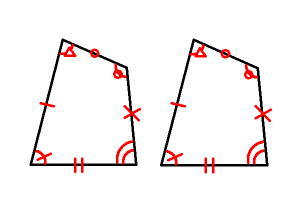



合同な図形の性質
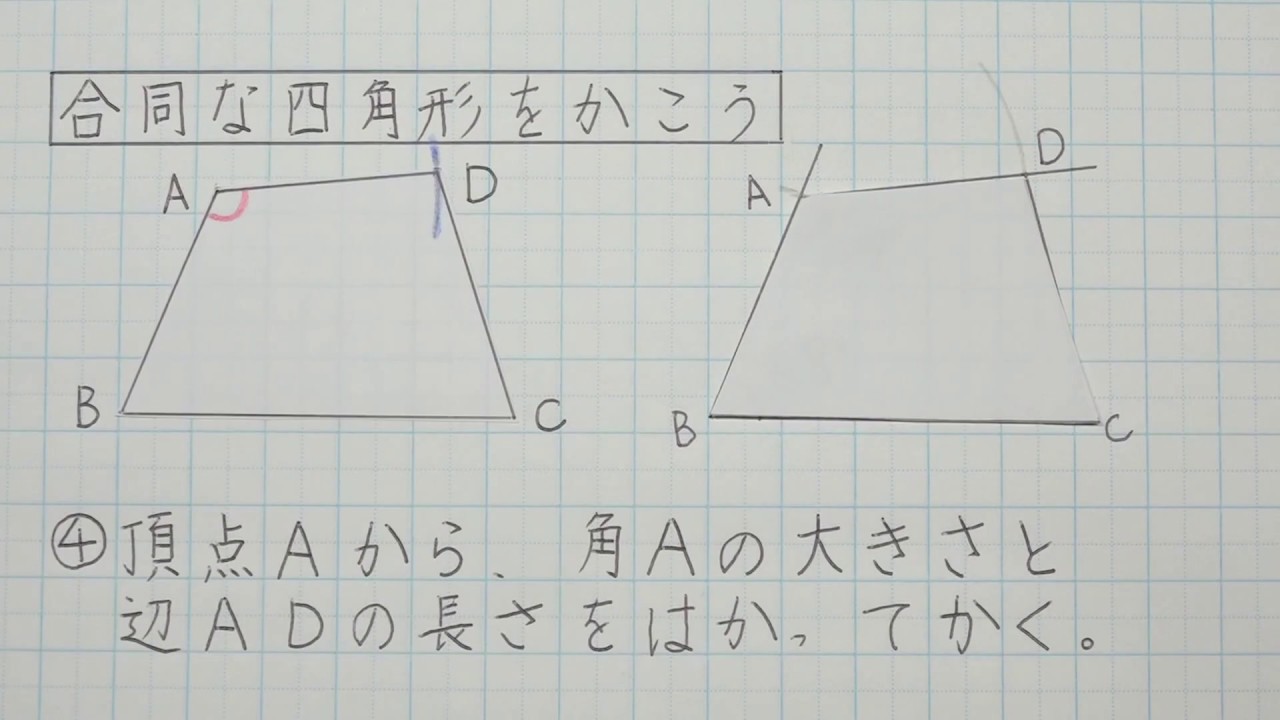



5年算数 図形の角と合同 5 合同な四角形をかこう Youtube



1




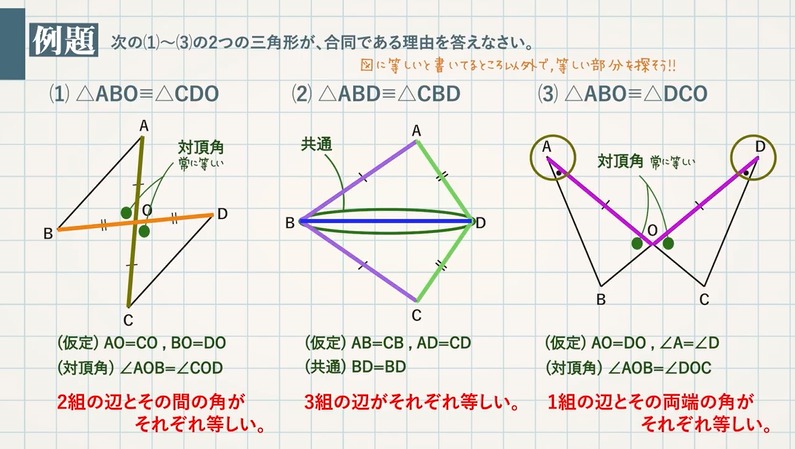
無料 中2数学 標準問題 解答プリント 225 図形5 仮定と結論




三角形の合同条件と証明問題の解き方 数学fun
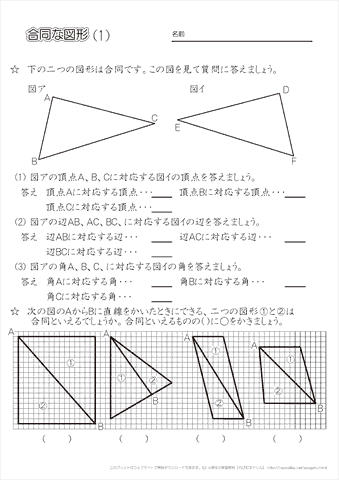



小学5年生の算数 合同な図形の性質を知る 練習プリント ちびむすドリル 小学生



5年算数合同な図形 わかる教え方




世界一分かりやすい算数 小5 合同な図形
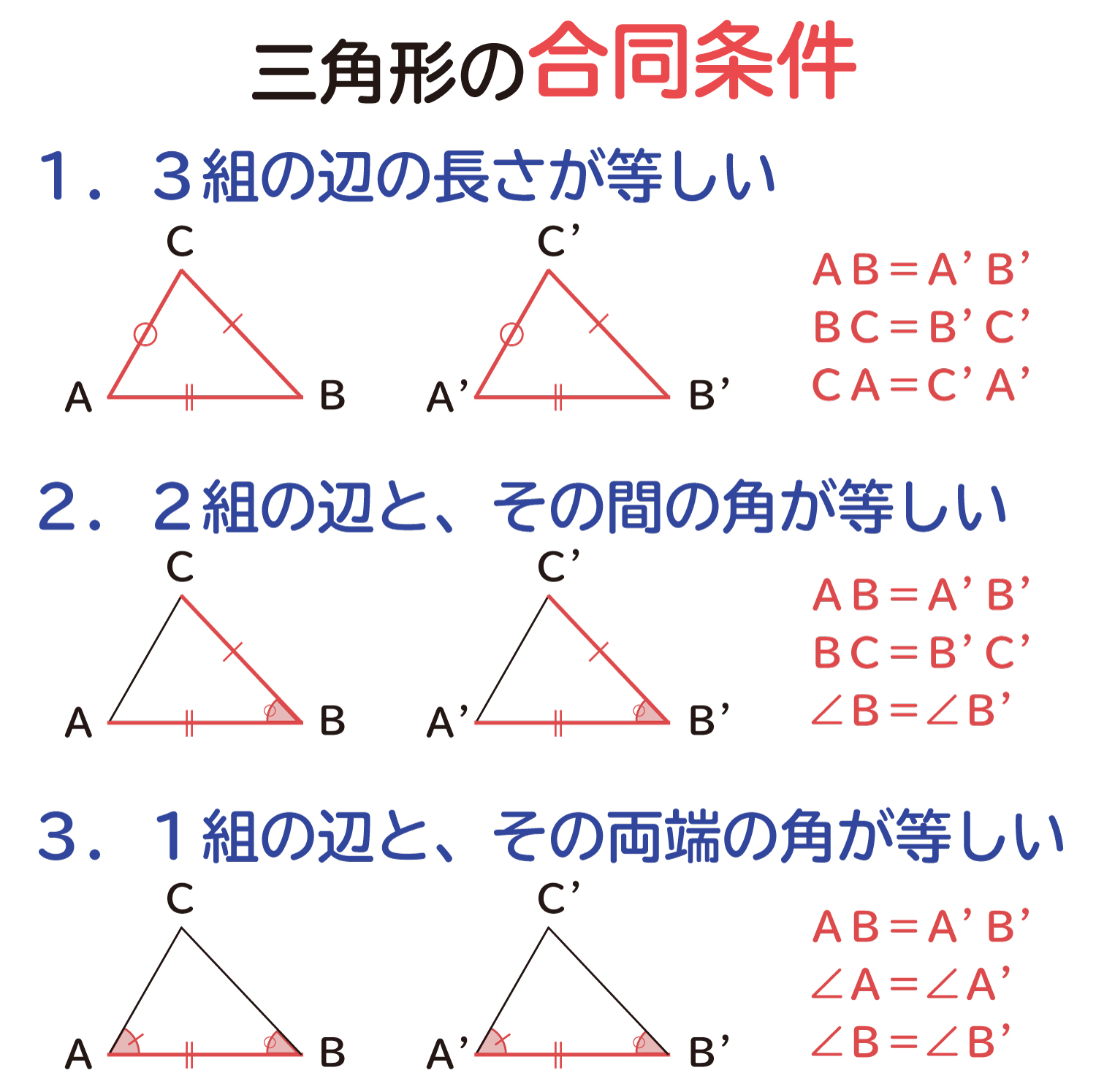



三角形の合同条件の説明 おかわりドリル



算数 合同な図形 三角形の角 黒板log



Http Www Fuchu03s Fuchu Tokyo Ed Jp Files Items File 5 E5 B9 B4 E7 Ae 97 E6 95 B0 Pdf




中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン



算数 合同な図形 三角形の角 黒板log
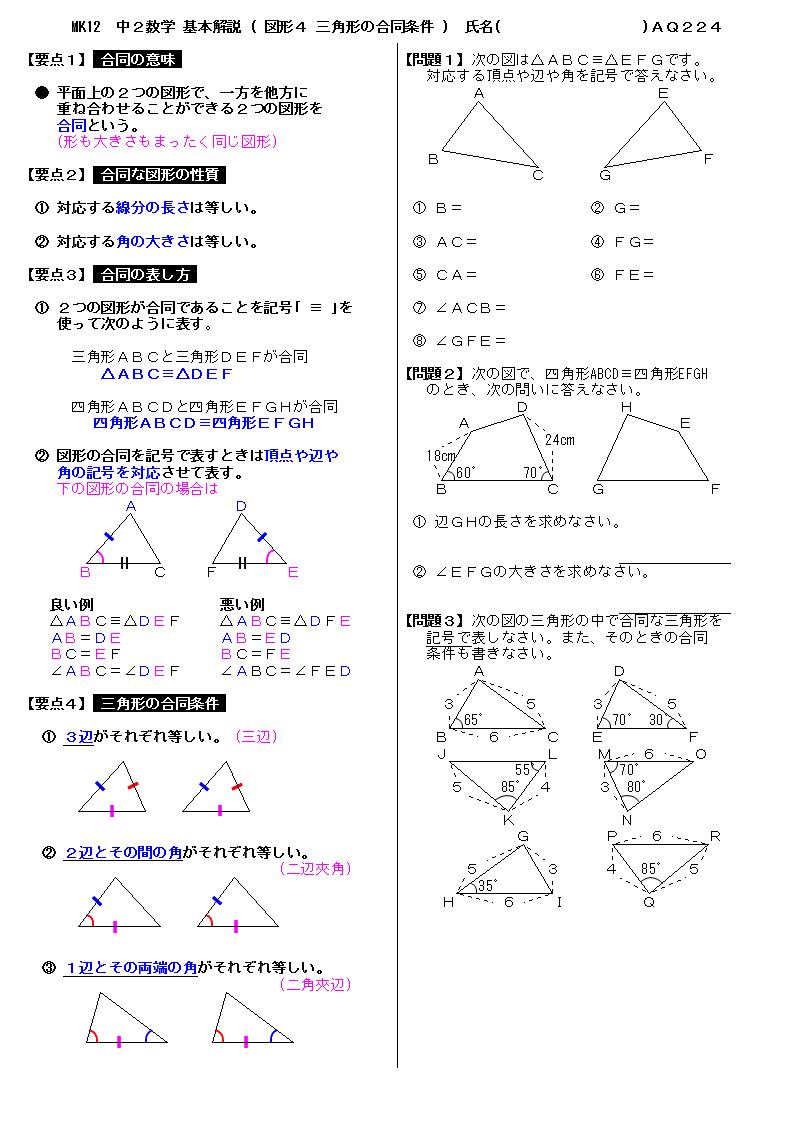



無料 中2数学 基本解説 問題プリント 224 図形4 三角形の合同条件




スズ 数学復習 Flashcards Quizlet




5年算数 図形の角と合同 3 四角形を対角線に分けて 合同な三角形を作ろう あなたの人生はあなたの思い描いたとおりになる



4章 図形の性質と合同 タカラゼミ




重なる形と図形の角を調べよう 図形の角と合同 第5学年 小学校 算数 My実践事例 日本文教出版



中2 数学 三角形の合同条件 角の和を求めてみよう Geogebra




三角形の合同条件
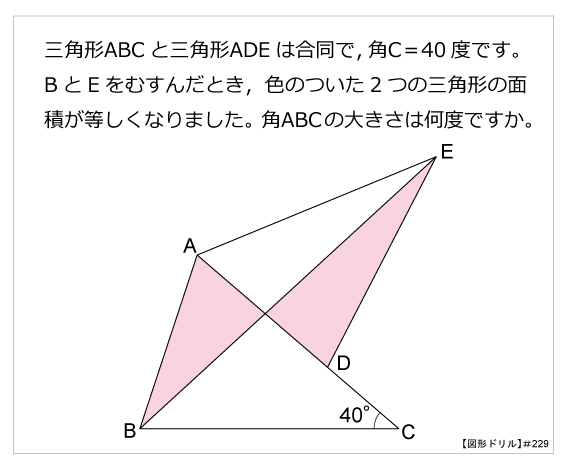



図形ドリル 第229問 合同な2つの三角形 算数星人のweb問題集 中学受験算数の問題に挑戦



記号にすると と 三角形の 合同 と 相似 の違いをまとめよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス




図形の合同 Wikipedia




合同な三角形の作図 2つの辺とその間の角 スクールプレゼンター用教材 教材 プリント 学びの場 Com



合同とは 相似とは




2 Descubre Como Resolverlo En Qanda




合同な図形の対応する頂点 辺 角について 5年算数 茎崎学園 つくば市立茎崎第二小学校




小5 算数 小5 15 合同な図形 Youtube




中2数学 同位角 錯角 対頂角 図形の合同 ひっそりと物理や数学を解説する



合同な図形2



小学5年生の算数 合同な図形の性質を知る 練習プリント ちびむすドリル 小学生



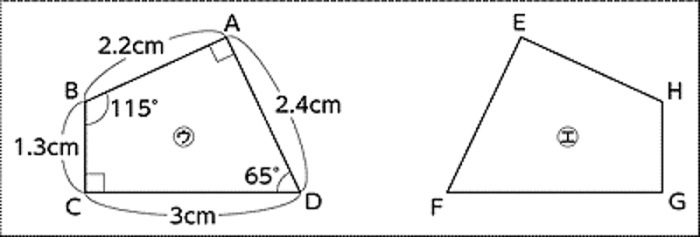
合同な図形の対応する角の答え方は対応順ってどういうこと まぜこぜ情報局



動画で学習 1 合同な図形 算数



1



図形の決定条件 算数用語集



Core Ac Uk Download Pdf Pdf



中学数学 図形の合同 図形の性質



合同な図形は色で学ぶと理解が深まる 算数数学が苦手な子専門のプロ家庭教師みかん先生




図形の合同と対応 算数用語集



3




三角形の合同条件



証明 合同 相似 が苦手な人へ 教遊者




旧バージョン 5年算数 図形の角と合同 4 合同な三角形をかこう Youtube




合同な図形の性質 三角形の合同とはどういう意味 Qikeru 学びを楽しくわかりやすく



5年算数合同な図形 わかる教え方




小学5年生 算数 7月 合同な図形 三角形と四角形の角度 偶数と奇数 倍数と公倍数 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ




中2数学 三角形の合同の証明の解き方の手順 こいがくぼ翼学習塾



4 図形の調べ方 1章 平行と合同 3 三角形の合同 2時間 Ppt Download



中学数学 図形の合同 図形の性質




すきるまドリル 小学5年生 算数 合同な図形 無料学習プリント すきるまドリル 無料学習プリント




世界一分かりやすい算数 小5 合同な図形



三角形の合同条件と証明問題の解き方 数学fun




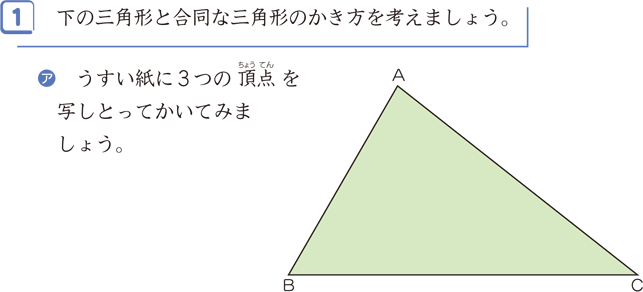
合同な三角形をかこう 家庭学習レシピ
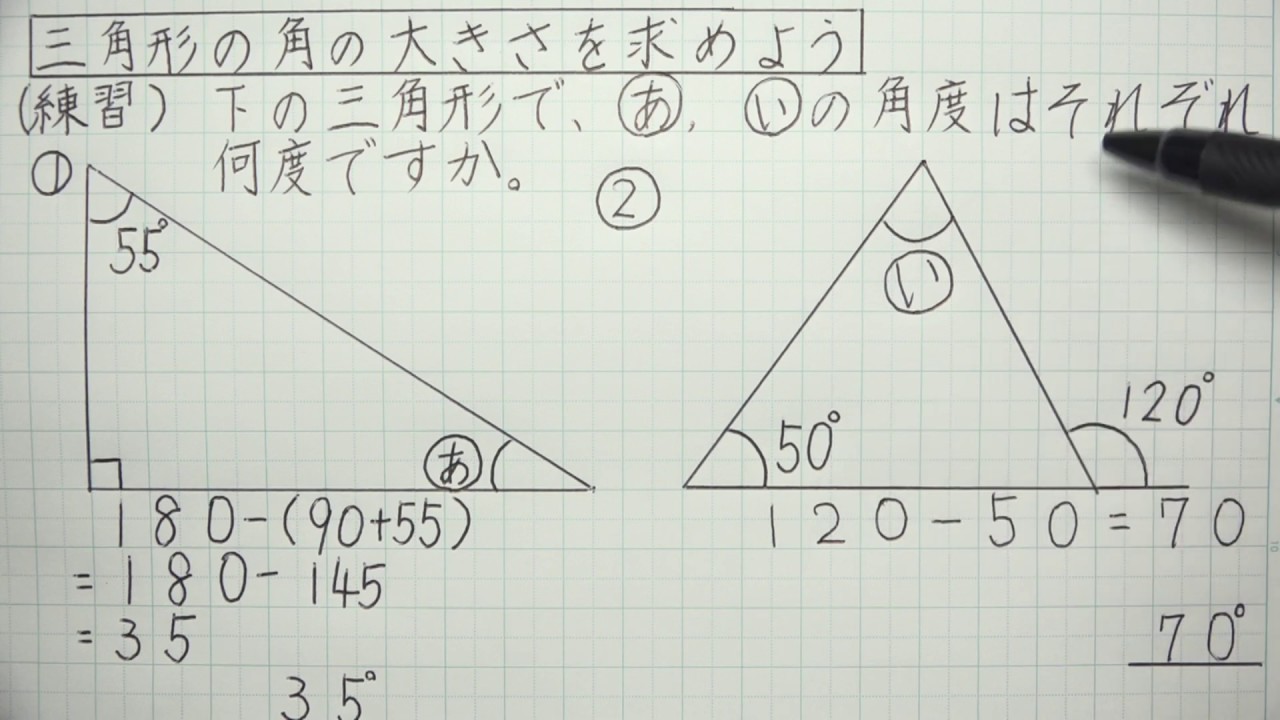



5年算数 図形の角と合同 6 三角形の角の大きさを求めよう Youtube



Wordで使える 共通な角 の三角形の合同の図 Wordで数学問題プリントを作ろう



対応する角 は色分けで視覚サポートが大切 はロックされています 対応する角 は色分けで視覚サポートが大切 図式




旧バージョン 5年算数 図形の角と合同 6 三角形の3つの角の大きさの和を調べよう Youtube




5年算数 図形の角と合同 7 いろいろな方法で合同な四角形をかこう あなたの人生はあなたの思い描いたとおりになる




三角形の合同条件と証明問題の解き方 数学fun



5年算数合同な図形 わかる教え方



1



2
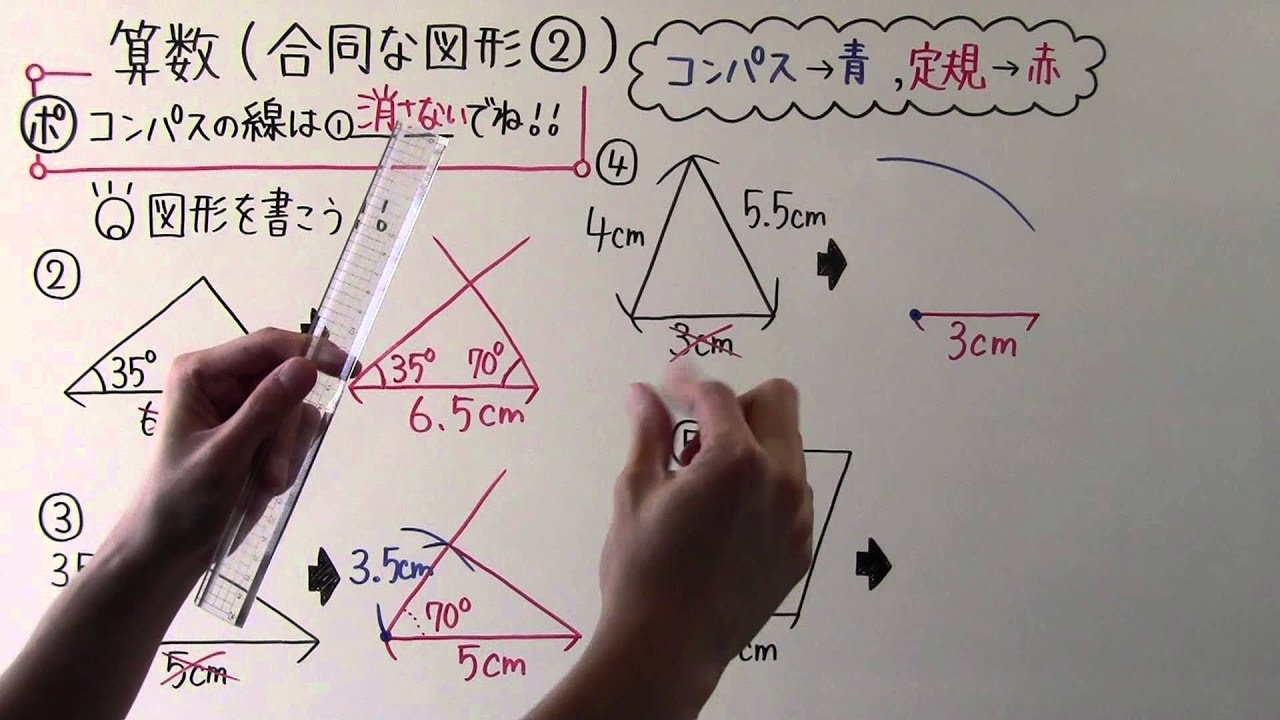



小5 算数 小5 16 合同な図形 Youtube



対応する辺を見つけるには 教育考現学




5年算数 図形の角と合同 7 いろいろな方法で合同な四角形をかこう あなたの人生はあなたの思い描いたとおりになる



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Cc100 Sannsuu Documents S5 024 Pdf




中2数学 図形の調べ方 中学生 数学のノート Clear
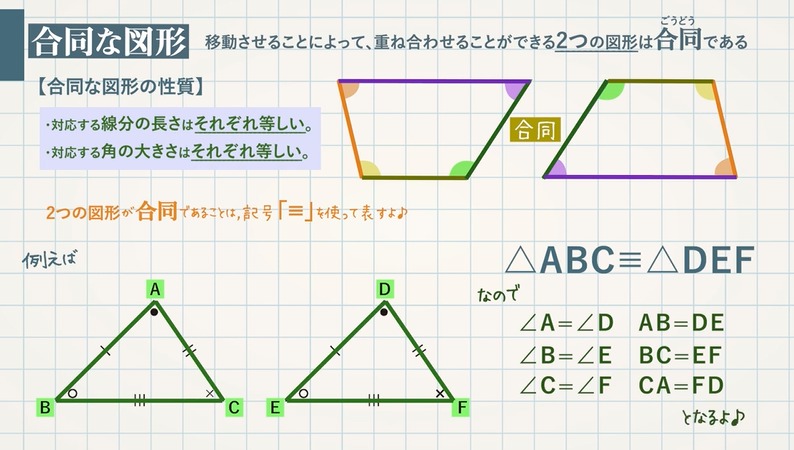



合同な図形とは 三角形の合同条件 教遊者




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学
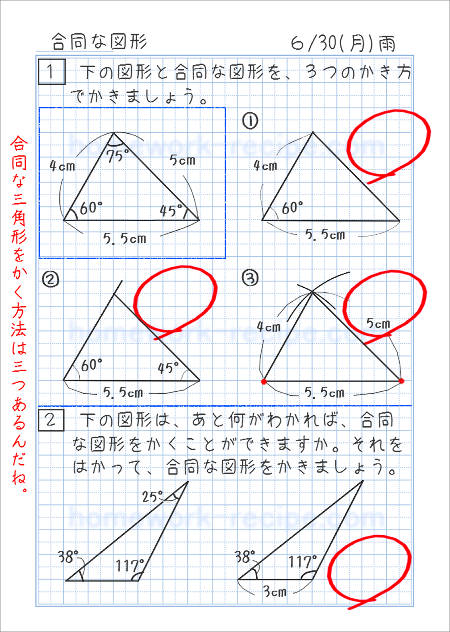



合同な三角形をかこう 家庭学習レシピ



小学5年生の算数 合同な図形 について教えてください 画像添付の問題なのですが Yahoo 知恵袋



Http Www Kita9 Ed Jp Eductr Handbook Challengesheet Elementaryschool Sansuu 5 506 Pdf




中学数学 合同な図形の性質とは 見つけ方は 問題を使って解説 数スタ
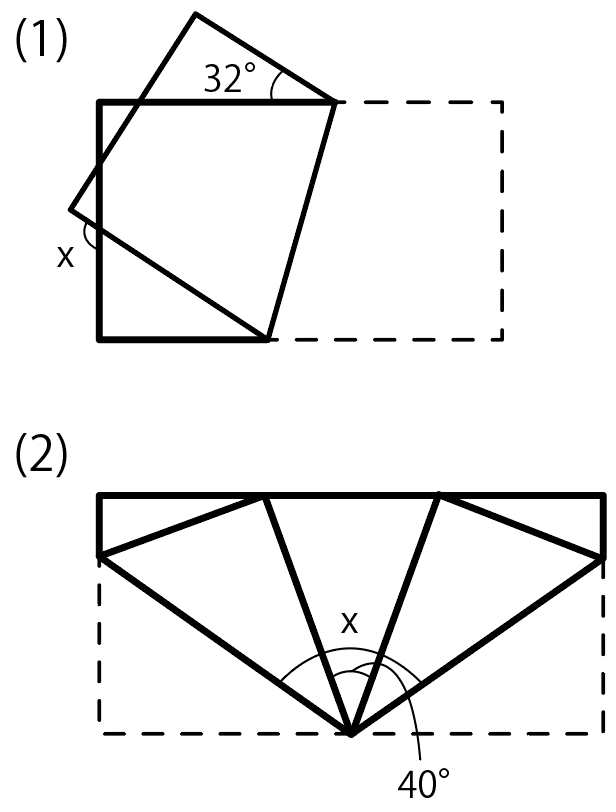



折り返した図形の角度を求める2つのコツ Qikeru 学びを楽しくわかりやすく
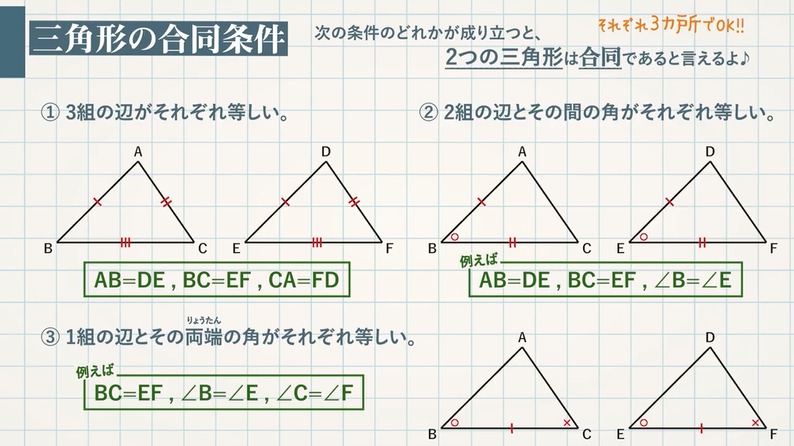



合同な図形とは 三角形の合同条件 教遊者



算数 合同な図形 導入 合同な図形の描き方 まで 黒板log




無料 中2数学 標準問題 解答プリント 227 図形7 復習
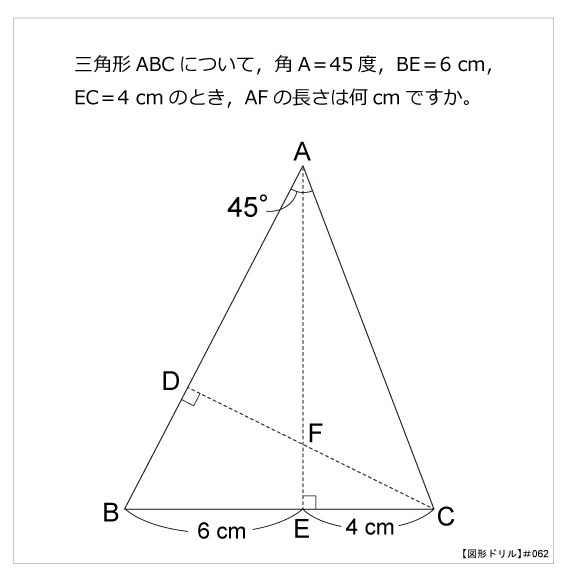



図形ドリル 第62問 合同の発見 算数星人のweb問題集 中学受験算数の問題に挑戦




中2 数学 角と平行線 三角形の合同 重要語句 円周角含む 中学生 数学のノート Clear
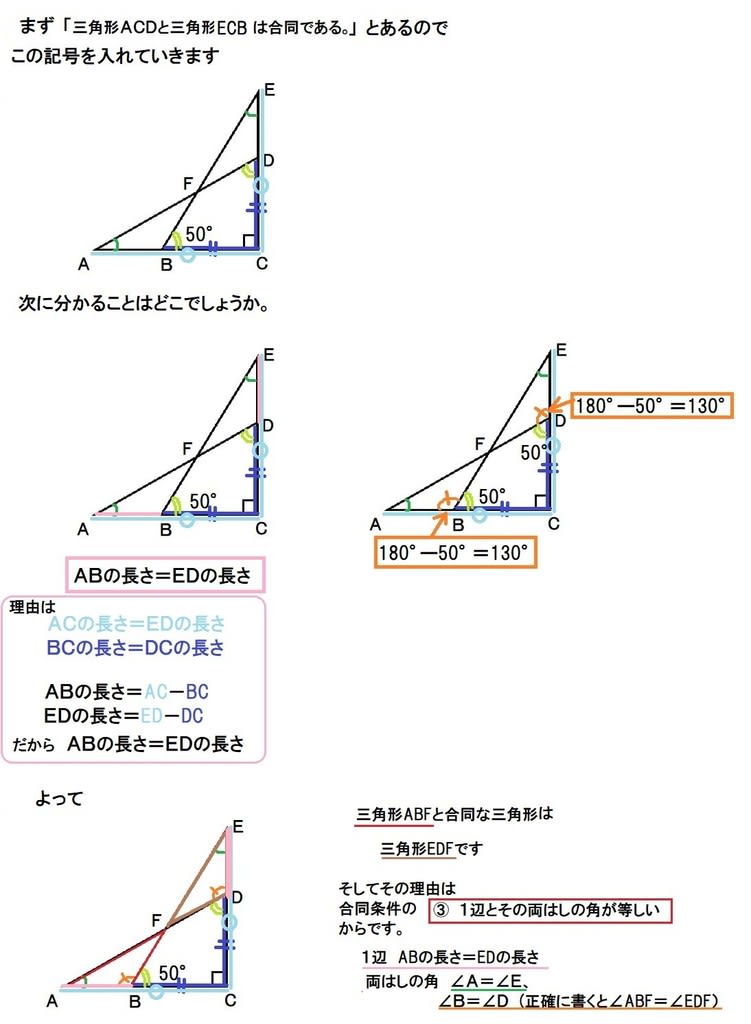



合同な図形 小5 合同条件は超重要 算数の教え方教えますmother S Math Happy Study Support
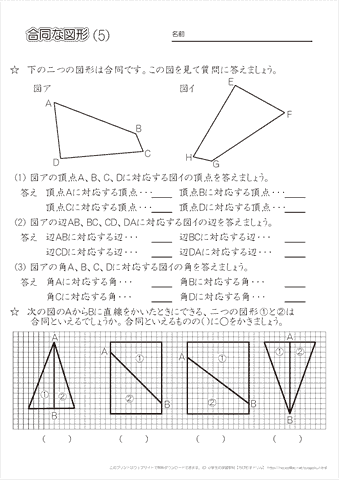



小学5年生の算数 合同な図形の性質を知る 練習プリント ちびむすドリル 小学生




すきるまドリル 小学5年生 算数 合同な図形 無料学習プリント すきるまドリル 無料学習プリント



合同な図形2




旧バージョン 5年算数 図形の角と合同 6 三角形の角の大きさを求めよう Youtube



Www Hokkyodai Ac Jp Files H24 5 Sansuu Pdf
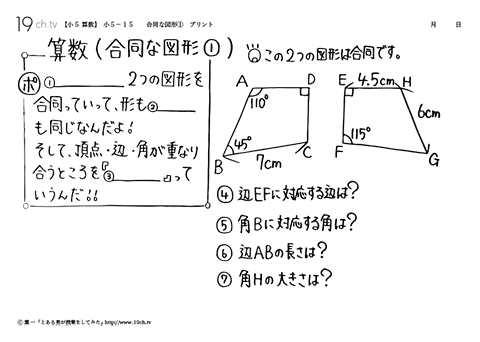



小学5年生の算数 動画 合同な図形 の問題 19ch
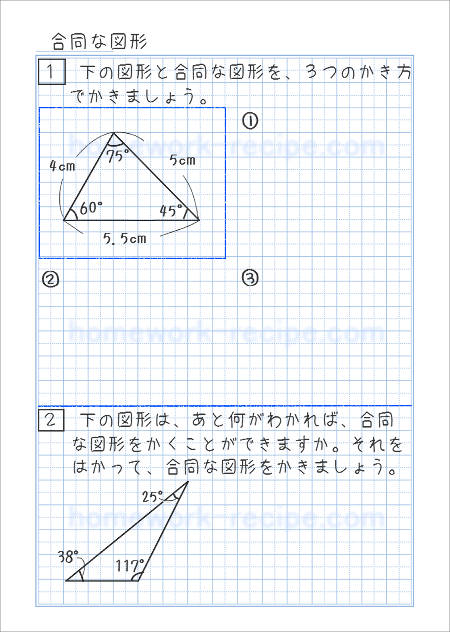



合同な三角形をかこう 家庭学習レシピ
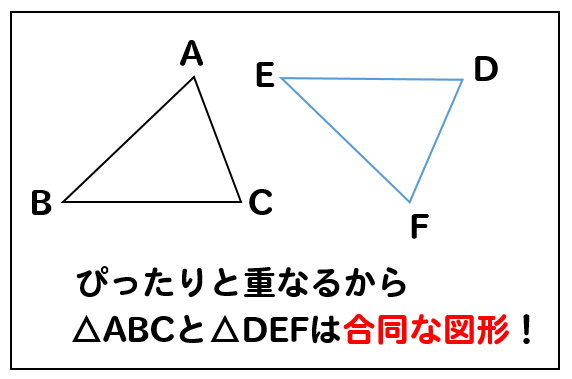



中学数学 合同な図形の性質とは 見つけ方は 問題を使って解説 数スタ
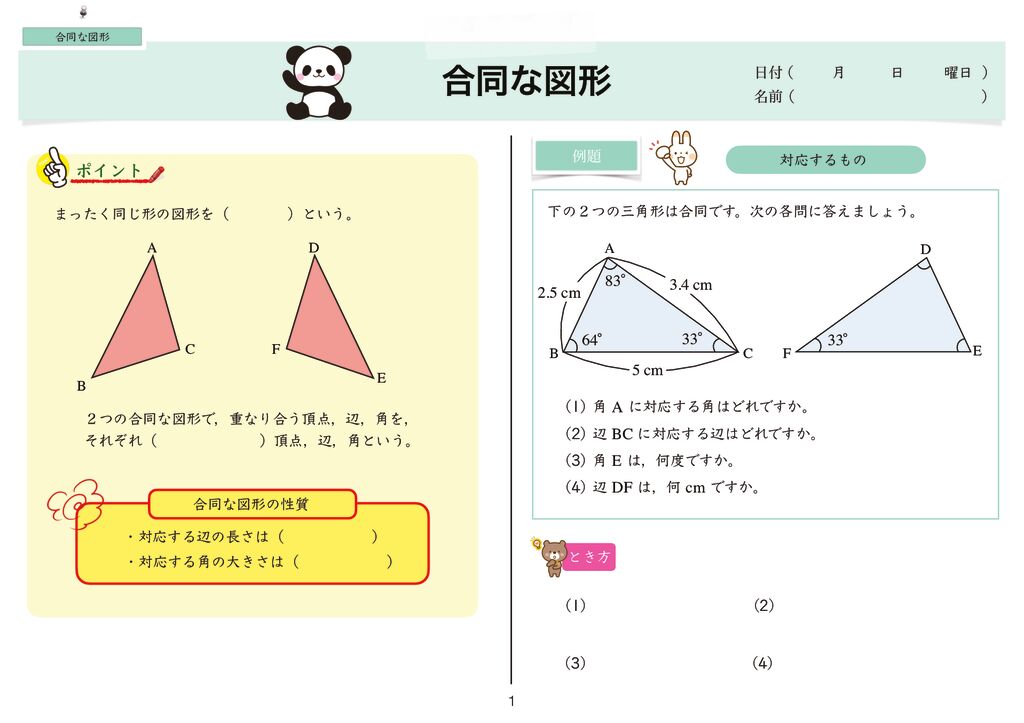



世界一分かりやすい算数 小5 合同な図形



5年生 算数 図形の合同 小学生の勉強法 親子学びスクール


